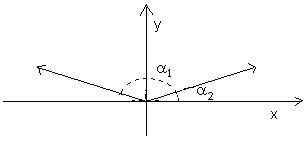
a 2 = 180° - a 1
Funzione inversa di y=senx
Risposta
a) b deve appartenere all'intervallo [-1,1]; infatti se
non vi appartiene il problema non ha soluzione.
Disegna dei vettori unitari la cui componente
verticale è 0.4. Quanti ce ne sono?
Il seno degli angoli che tali vettori formano
con l'asse x è 0.4?
Quale relazione c'è tra gli angoli che
essi formano con l'asse x?

a 2 = 180° - a 1
Risposta
c) In generale per ogni valore di b Î
[-1,1] si trovano due angoli a1
ea2
Î[0;2p
] tali che sen a 1
= b e sen a2
= b. Infatti
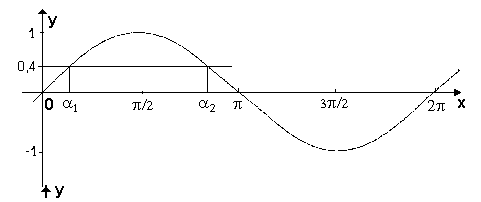
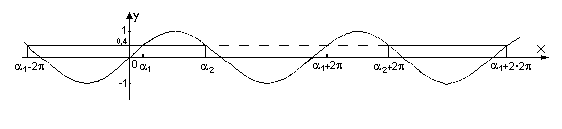
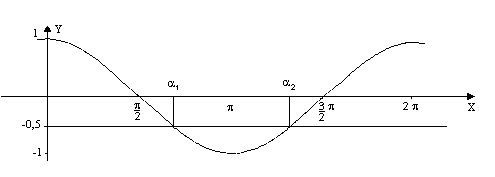
Utilizzando la sinusoide determina graficamente quanti angoli hanno il seno uguale a -0.6.
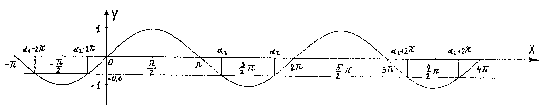
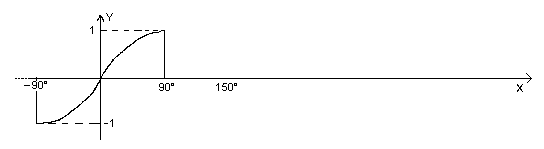
Ad ogni valore di b Î [-1,1] corrisponde un solo valore dell'angolo Î [-90°,90°], quindi la funzione y = sen x è invertibile nell'intervallo [-90°,90°].
Completa la seconda tabella scambiando la x con la y
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
Con l'uso della calcolatrice, pigiando i tasti opportuni, riempi i posti vuoti nel seguente schema:
|
|
|
|
| 60° | ® | ® |
| 120° | ® | ® |
| 240° | ® | ® |
| 300° | ® | ® |
Di un angolo a
hai queste informazioni: 0°< a
< 90° e sen a
= 0.866; determina a,
usando la calcolatrice.
Di un angolo a
hai queste informazioni: 0°< a
< 360° e sen a
= 0.866; determina a,
con l'aiuto della calcolatrice. Quanti valori di a
hai trovato?
Risolvi in (0°; 360°)
|
sen a = 0.75 |
sen a
= -0.8
sen a = -0.25 |
a1 = acalcolatrice a2 = 180° - acalcolatrice
Calcolando per mezzo della calcolatrice arcsen (-0.8)
si ottiene - 53° che non appartiene all'intervallo [0°;360°).
Sfruttando la periodicità della funzione y = sen
x una soluzione è data da 360° + (-53°) = 307°. L'altra
soluzione è data da 180° - ( - 53° ) = 233°.
In generale se sen a
< 0
a è l'angolo
maggiore di un triangolo ottusangolo, sapendo che sen a
= 0.9, determina a.
a è un angolo
di un triangolo, sapendo che sen a
= 0.7, determina a.
a, b
, g sono angoli di
un triangolo:
a) se sen a
= 0.5, b = 100°,
determina a
b) se g
è acuto, sen a
= 0.5, sen b = 0.71 determina
a e b
c) sen a
= 0.5 , sen b= 0.5,
sen g= 0.866, determina
a,
b
, g
d) se sen a
= 0.94, sen b = 0.77,
determina a, b
, g
e) se sen a
= 0.94, sen b = 0.77,
sen g= 0.34, determina
a,
b
, g
f) se sen a
= 0.94, sen b = 0.77,
sen g = 0.866, determina
a,
b
, g
Risposta
a) b deve appartenere all'intervallo [-1,1]; infatti se
non vi appartiene il problema non ha soluzione.
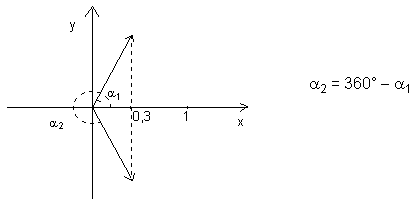
Risposta
In generale per ogni valore di bÎ[-1,1]
si trovano due angolia1
e a2Î
[0;2p ] tali che cos
a1
= b e cos a2
= b. Infatti
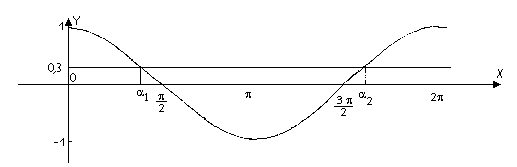
Utilizzando la cosinusoide determina graficamente quanti angoli hanno il coseno uguale a 0.3.
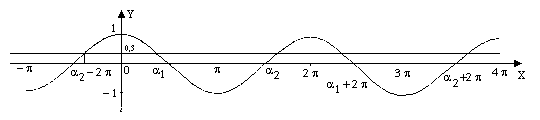
![]() ®
®
![]()
Se b = 0.3 cosa compare sul visore? Confronta tali
valori con i risultati dell'esercizio 6.1. La calcolatrice ha scelto l'angolo
che si trova tra 0° e 180°.
Se b = -0.5 cosa compare sul visore? Confronta con
i risultati dell'esercizio 6.2. La calcolatrice ha scelto l'angolo compreso
tra 0° e 180°.
In generale possiamo dire che la calcolatrice, tra
tutti gli angoli possibili, ha fatto corrispondere sempre quello positivo
più vicino allo zero.
Ritorniamo al grafico
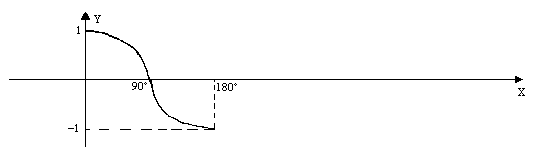
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
Con l'uso della calcolatrice, pigiando i tasti opportuni, riempi i posti vuoti nel seguente schema:
|
|
|
|
| 60° | ® | ® |
| 120° | ® | ® |
| 240° | ® | ® |
| 300° | ® | ® |
Di un angolo a hai queste informazioni: 0°<a< 90° e cos a = 0.866; determina a.
Di un angolo a
hai queste informazioni: 0°< a
< 360° e cos a
= 0.866; determina a.
Quanti valori di a
hai trovato?
Risolvi in (0°; 360°)
|
cos a = 0.65 |
cos a = -0.15 |
Le rette parallele all'asse x incontrano il grafico di y = tanx in infiniti punti.
Trasformiamo i gradi in radianti. La
funzione inversa di y = tanx si chiama y = arctanx, ha dominio (-¥
;+¥ ) e codominio
(-p /2;p /2).
A partire dalla tabella dell'esercizio
7.5 compila una tabella relativa alla funzione y = arctanx e rappresentala
graficamente.
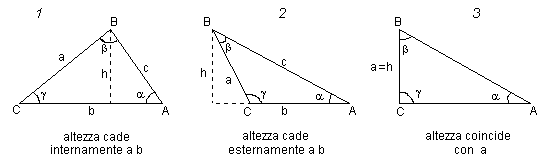
| Caso 1) | h = a sen g | quindi A = 1/2 b a sen Y |
| Caso 2) | h = a sen(180°- g ) = a sen g | quindi A = 1/2 b a sen g |
| Caso 3) | h = a quindi A = 1/2 a b
ma sen g= sen 90° = 1 |
quindi A = 1/2 a b ma sen g = sen 90° = 1 |
Scrivi le formule analoghe per l'area
riferendole a tutte le coppie possibili di lati.
In base alle formule precedenti si può scrivere:
Possiamo scrivere le uguaglianze precedenti nel seguente modo:
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
a² = b² + c² - 2bc cosa
Si possono presentare i seguenti casi:
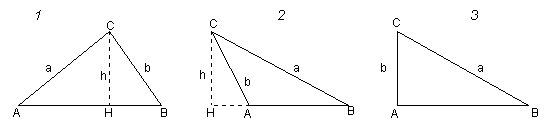
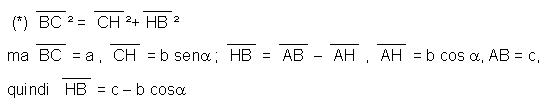
a² = (b sena)²
+ (c - b cosa)²
a² = b²sen²a
+ c² + b²cos²a
- 2bc cosa
a² = b²(sen²a
+ cos²a) + c²
- 2bc cosa
poiché sen²a
+ cos²a = 1 si
ottiene
a² = b² + c² - 2bc cosa

Scrivi le formule analoghe relative
ai lati b e c.
A cosa serve il teorema di Carnot.
Osservazione:
Il teorema dei seni e il teorema di Carnot ci permettono
di risolvere qualsiasi triangolo noti tre elementi di cui uno almeno sia
un lato.
Determina l'ampiezza degli angoli di
un triangolo avente lati di 10 cm, 12 cm, 14 cm.
Determina l'ampiezza degli angoli di
un triangolo avente i lati di 25 cm, 12 cm e 18 cm.
1° modo) Usa soltanto il teorema del
coseno.
2° modo) Usa il teorema del coseno
relativo all'angolo minore (cioè compreso tra i lati di 25 e 18
cm) e successivamente il teorema dei seni.
Confronta i risultati ottenuti.
Osservazione:
Strategia Vincente: conoscendo i tre lati
di un triangolo conviene innanzitutto determinare l'angolo maggiore col
teorema del coseno e gli altri angoli col metodo che vuoi.
Determina l'ampiezza degli angoli di un triangolo avente i lati di 5 cm, 6 cm e 15 cm. Segui la strategia vincente.
Osservazione:
Ti sarai accorto che cos a
è un numero minore di -1. Ciò non è possibile. Il
triangolo non esiste, infatti la somma di due lati è minore del
terzo.
In un triangolo due lati misurano 11 cm, e 10 cm e l'angolo opposto al maggiore misura 55°, determina l'altro lato e gli angoli.
Osservazione:
Se di un triangolo si conoscono due lati
e l'angolo opposto al maggiore il triangolo è sempre risolubile
e in un sol modo.
In un triangolo due lati misurano rispettivamente
11 cm e 10 cm e l'angolo opposto al lato minore misura 55 , determina l'altro
lato e gli angoli.
In un triangolo due lati misurano rispettivamente
11 cm e 10 cm e l'angolo opposto al lato minore misura 80°. Determina
l'altro lato e gli altri angoli.
In un triangolo due lati misurano rispettivamente 37 cm e 35 cm e l'angolo opposto al lato minore misura 71°. Determina l'altro lato e gli altri angoli.
Osservazioni:
Se di un triangolo conosciamo due lati
e l'angolo opposto al minore, per risolvere il triangolo possono presentarsi
due casi:
Se esaminiamo gli esercizi in cui esiste una sola soluzione possiamo ricordare che due triangoli sono uguali se